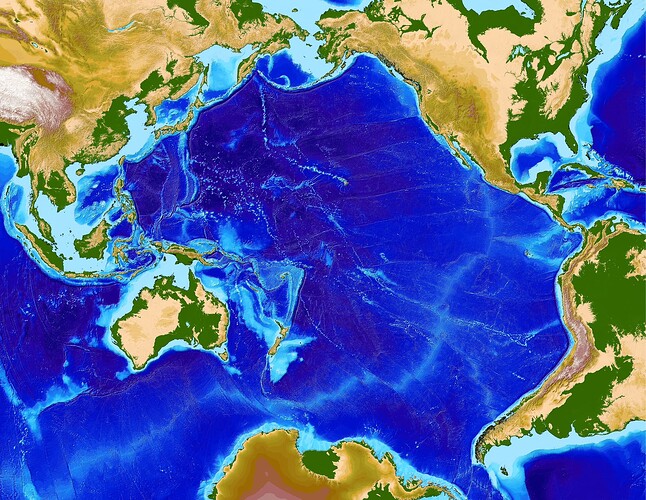
This is the most hideous bash script in the world below. It annotates the frames and draws grid lines on the Oblated Stereographic map of the Pacific. It really would be better in a language like Julia. But it works.
To get the annotations on the frame, I created lists of (Lon, lat) for the points along the edge, and then used gmt sample1d to interpolate to evenly spaced latitudes or longitudes. But the catch was gmt sample1d expects monotonically increasing or decreasing data. So I need to break the lists of latitudes and longitudes up into individual files where this monotonic requirement is met.
Unfortunately I cannot upload any images to the forum at the moment - is something broken? The map is starting to look quite nice.
#!/usr/bin/env bash
proj="+proj=lee_os +ellps=GRS80"
proj_region="-R-10674773/10691707/-8028940/8499687"
geog_region="-R70/330/-90/80"
function grid(){
local spc="${2}"
for lat in $(seq -80 10 80)
do
echo ">"
gmt math -T70/330/1 ${lat} = | gmt mapproject -J"${proj}" ${geog_region}
done
for lon in $(seq 70 10 330)
do
echo ">"
gmt math -o1,0 -T-90/80/1 ${lon} = | gmt mapproject -J"${proj}" ${geog_region}
done
}
function monotonic(){
local col="${1}"
local spc="${2}"
awk -v spc="${spc}" -v col="${col}" '
{
if (col == 3){
val = ($col < 0) ? $col + 360 : $col;
} else {
val = $col;
}
}
NR==1{
file_num = 1;
file=sprintf("labels_%04d.txt", file_num)
printf("%f\t%f\t%f\n", $1, $2, val) > file;
prev_val = val;
}
NR==2{
incdec = val-prev_val;
printf("%f\t%f\t%f\n", $1, $2, val) > file;
prev_val = val;
}
NR>2{
if (((val <= prev_val)&&(incdec < 0)) || ((val >= prev_val) && (incdec >= 0))){
printf("%f\t%f\t%f\n", $1, $2, val) > file;
prev_val = val
} else {
file_num++;
file=sprintf("labels_%04d.txt", file_num)
incdec = val-prev_val;
printf("%f\t%f\t%f\n", $1, $2, val) > file;
prev_val = val;
}
}'
}
function frame(){
local region=$1
local edge=$2
local ll=$3
local spc=$4
case "${edge}" in
"west")
local order="1,0"
local min=$(echo "${region}" | cut -d "/" -f 3)
local max=$(echo "${region}" | cut -d "/" -f 4)
local border=$(echo "${region}" | cut -d "/" -f 1)
;;
"east")
local order="1,0"
local min=$(echo "${region}" | cut -d "/" -f 3)
local max=$(echo "${region}" | cut -d "/" -f 4)
local border=$(echo "${region}" | cut -d "/" -f 2)
;;
"south")
local order="0,1"
local min=$(echo "${region}" | cut -d "/" -f 1)
local max=$(echo "${region}" | cut -d "/" -f 2)
local border=$(echo "${region}" | cut -d "/" -f 3)
;;
"north")
local order="0,1"
local min=$(echo "${region}" | cut -d "/" -f 1)
local max=$(echo "${region}" | cut -d "/" -f 2)
local border=$(echo "${region}" | cut -d "/" -f 4)
;;
esac
if [[ "${ll}" == "lon" ]]
then
local col=3;
else
local col=4;
fi
gmt math -o"${order}" -T${min}/${max}/10000 ${border} = label.xy
gmt mapproject -I -J"${proj}" < label.xy > label.ll
rm -f labels_????.txt
paste label.xy label.ll | monotonic "${col}" "${spc}"
ls -1 labels_????.txt | xargs -I file gmt sample1d file -N2 -T${spc} | awk \
-v ll="${ll}" '
{
val=$3;
if (ll == "lon"){
if (val > 180){
valstr=sprintf("%.f\260W", 360-val);
} else {
valstr=sprintf("%.f\260E", val);
}
} else {
if (val < 0){
valstr=sprintf("%.f\260S", -1*val);
} else {
valstr=sprintf("%.f\260N", val);
}
}
printf("%f\t%f\t%s\n", $1, $2, valstr);
}'
}
#gmt mapproject pacific_500m.gmt -J"${proj}" ${geog_region} -bi2f -bo2f > coast.gmt
#gmt grdcut @earth_relief_30s ${geog_region} -Gtopo.nc
#gmt grd2xyz topo.nc | gmt mapproject -J"${proj}" ${geog_region} -bo3f | \
# gmt blockmean -I1000/1000 -R-10675000/10692000/-8029000/8500000 -bi3f -bo3f | \
# gmt surface -I1000/1000 -R-10675000/10692000/-8029000/8500000 \
# -Ll-11000 -Lu9000 -Gpactopo.nc -bi3f
#gmt grd2xyz topo.nc | gmt mapproject -J"${proj}" ${geog_region} -bo3f | \
# gmt nearneighbor -I1000/1000 -R-10675000/10692000/-8029000/8500000 \
# -S5000 -bi3f -Gpactopo.nc
gmt begin pacific PNG
gmt grdimage pactopo.nc -Jx1:50000000 ${proj_region} -Cetopo1 -I
gmt plot coast.gmt -Jx1:50000000 ${proj_region} -Wfaint,black -bi2f
grid 10 | gmt plot -Wthinnest,white,.
frame "-10675000/10692000/-8029000/8500000" "west" "lat" 10 | \
gmt text -Jx1:50000000 ${proj_region} -F+a0+jLM+f8p,Helvetica,white \
-N -Dj0.2c/0c
frame "-10675000/10692000/-8029000/8500000" "north" "lon" 10 | \
gmt text -Jx1:50000000 ${proj_region} -F+a90+jRM+f8p,Helvetica,white \
-N -Dj0.2c/0c
frame "-10675000/10692000/-8029000/8500000" "east" "lat" 10 | \
gmt text -Jx1:50000000 ${proj_region} -F+a0+jRM+f8p,Helvetica,white \
-N -Dj0.2c/0c
gmt end
. A quick search found Copernicus is highly regarded: 
I have an idea for adding them all, without that much difficulty, I just haven’t got around to it yet.