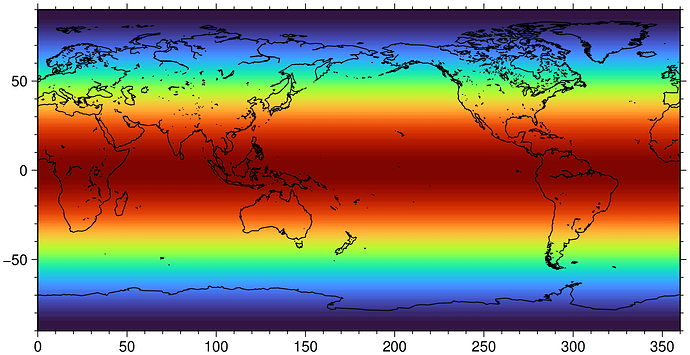
I want to create a grid of WGS84 ellipsoid (with the distance to the center of the earth).
I found that I could solve this equation where the “radii” is a function of the latitude.

a: mayor axis
b: minor axis
Is there any module that have this formula already incorporate? mapproject?
Or should I do it from scratch?
Seems like a grdmath macro you create and stick in ~/.gmt/grdmath,macros, e.g.
# Accept a b and evaluate ellipsoid on the grid
ELLIPSOID = STO@a POP STO@b POP RCL@a 2 POW Y COSD MUL 2 POW RCL@b 2 POW Y SIND MUL 2 POW ADD etc etc
then
gmt grdmath -Rg -I1 6378137.0 6356752.3142 ELLIPSOID = my.grd
1 Like
I have many macros for grdmath and gmtmath - perhaps we should show people how to do these things. I am sure only 0.00044% of GMT users are even aware of this capability.
4 Likes
Sure, because compare that with
julia> a = 6378137.0;
julia> b = 6356752.3142;
julia> phi = -90:1:90;
julia> f(phi) = sqrt.( ((a^2 * cosd.(phi)).^2 .+ (b^2 * sind.(phi)).^2) ./ ((a * cosd.(phi)).^2 .+ (b * sind.(phi)).^2) )
f (generic function with 1 method)
julia> col = f(phi);
julia> mat = repeat(col,1,361);
julia> G = mat2grid(mat, hdr=[0,360,-90,90, b, a, 0, 1, 1]);
imshow(G, coast=true)
1 Like
Never knew this; please do.
Yes, but now we are talking apples and oranges. We can do the same in matlab and python. And the amount of coding in those languages are not necessarily less - usually RPN expressions are more compact.
“More compact” does not necessarily mean “easier to implement” or “more readable/understandable” for each particular user. Often means “more error-prone” and “very steep learning curve”.
I have many macros for grdmath and gmtmath - perhaps we should show people how to do these things.
please do, would be much appreciated.
@mkononets said most of what wanted. The problem with grdmath for equations is it quickly becomes very complex to incomprehensible. I don’t imagine the time it would take me to write that expression.
Fair enough. I speak fluent RPN 
Many thanks to all the answers.
I just wonder if Julia can translate any formula into RPN (if it is good as they said).
Julia is a programming language and like any programming languages it does nothing by itself. It’s people (and now other programs too) who write programs to achieve the wished objectives.
But what would be the interest in translating a formula to RPN when the idea is to execute that formula?
Just curious. But it could be helpfull as an interactive tool to learn RPN.
My impression that grdmath has been created when there was nothing like Python/Julya around with rich native libraries greatly simplifying processing of netcdf grid files and the like.
I am more curious to see what people like Pål do with grids using grdmath rather than exactly how to do it with grdmath.
It was easier than I expected.
ELLIPSOID = STO@a POP STO@b POP RCL@a 2 POW Y COSD MUL 2 POW RCL@b 2 POW Y SIND MUL 2 POW ADD RCL@a Y COSD MUL 2 POW RCL@b Y SIND MUL 2 POW ADD DIV SQRT
then
gmt grdmath -Rg -I1 6378137.0 6356752.3142 ELLIPSOID = my.grd
Now I wonder if any way to extract the values of the elipsoid from GMT. I
I can list the values of the elipsoids with gmt mapproject -Qe. Is any way to take those values as inputs (instead of writing them in the formula)?
ID Date a 1/f
->WGS-84 1984 6378137.000 298.25722356
Well, you could have your macro expect a and 1/f and start by computing b = a (1-f) and keep the rest. e.g.
STO@a POP INV 1 SUB NEG RCL@a MUL STO@b POP …
Sorry, my doubt is how to extract the info (values a and 1/f) from the table.
The actual ouptut of gmt mapproject -Qe is:
GMT supports 76 ellipsoids, given below (-> indicates default setting)
ID Date a 1/f
-----------------------------------------------------------
Airy 1830 6377563.396 299.324964600
Airy-Ireland 1830 6377340.189 299.324964600
Andrae 1876 6377104.430 300.000000000
APL4.9 1965 6378137.000 298.250000000
ATS77 1977 6378135.000 298.257000000
Australian 1965 6378160.000 298.250000000
Bessel 1841 6377397.155 299.152812800
Bessel-Namibia 1841 6377483.865 299.152812800
Bessel-NGO1948 1841 6377492.018 299.152810000
Bessel-Schwazeck 1841 6377483.865 299.152812800
Clarke-1858 1858 6378293.639 294.260680000
Clarke-1866 1866 6378206.400 294.978698200
Clarke-1866-Michigan 1866 6378450.047 294.978698200
Clarke-1880 1880 6378249.145 293.465000000
Clarke-1880-Arc1950 1880 6378249.145 293.466307600
Clarke-1880-IGN 1880 6378249.200 293.466021300
Clarke-1880-Jamaica 1880 6378249.136 293.466310000
Clarke-1880-Merchich 1880 6378249.200 293.465980000
Clarke-1880-Palestine 1880 6378300.790 293.466230000
CPM 1799 6375738.700 334.290000000
Delambre 1810 6376428.000 311.500000000
Engelis 1985 6378136.050 298.256600000
Everest-1830 1830 6377276.345 300.801700000
Everest-1830-Kalianpur 1830 6377301.243 300.801740000
Everest-1830-Kertau 1830 6377304.063 300.801700000
Everest-1830-Pakistan 1830 6377309.613 300.801700000
Everest-1830-Timbalai 1830 6377298.556 300.801700000
Fischer-1960 1960 6378166.000 298.300000000
Fischer-1960-SouthAsia 1960 6378155.000 298.300000000
Fischer-1968 1968 6378150.000 298.300000000
FlatEarth 1984 6371008.771 inf
GRS-67 1967 6378160.000 298.247167427
GRS-80 1980 6378137.000 298.257222101
Hayford-1909 1909 6378388.000 297.000000000
Helmert-1906 1906 6378200.000 298.300000000
Hough 1960 6378270.000 297.000000000
Hughes-1980 1980 6378273.000 298.279400000
IAG-75 1975 6378140.000 298.257222000
Indonesian 1974 6378160.000 298.247000000
International-1924 1924 6378388.000 297.000000000
International-1967 1967 6378157.500 298.250000000
Kaula 1961 6378163.000 298.240000000
Krassovsky 1940 6378245.000 298.300000000
Lerch 1979 6378139.000 298.257000000
Maupertius 1738 6397300.000 191.000000000
Mercury-1960 1960 6378166.000 298.300000000
MERIT-83 1983 6378137.000 298.257000000
Modified-Airy 1830 6377340.189 299.324964600
Modified-Fischer-1960 1960 6378155.000 298.300000000
Modified-Mercury-1968 1968 6378150.000 298.300000000
NWL-10D 1972 6378135.000 298.260000000
NWL-9D 1966 6378145.000 298.250000000
OSU86F 1986 6378136.200 298.257220000
OSU91A 1991 6378136.300 298.257220000
Plessis 1817 6376523.000 308.640000000
SGS-85 1985 6378136.000 298.257000000
South-American 1969 6378160.000 298.250000000
Sphere 1984 6371008.771 inf
Struve 1860 6378297.000 294.730000000
TOPEX 1990 6378136.300 298.257000000
Walbeck 1819 6376896.000 302.780000000
War-Office 1926 6378300.583 296.000000000
WGS-60 1960 6378165.000 298.300000000
WGS-66 1966 6378145.000 298.250000000
WGS-72 1972 6378135.000 298.260000000
->WGS-84 1984 6378137.000 298.257223563
Web-Mercator 1984 6378137.000 inf
Moon 2000 1737400.000 inf
Mercury 2000 2439700.000 inf
Venus 2000 6051800.000 inf
Mars 2000 3396190.000 169.894447224
Jupiter 2000 71492000.000 15.414402760
Saturn 2000 60268000.000 10.207994580
Uranus 2000 25559000.000 43.616040956
Neptune 2000 24764000.000 58.543735225
Pluto 2000 1195000.000 inf
Well, presumably you know the name of the ellipsoid you want, e…, TOPEX so you will have to do
gmt mapproject -Qe 2>&1 | grep TOPEX
since mapproject writes that to stderr…
If you really need to automate ellipsoid building then I guess you could temporarily create a macro in the current directory? e.g.
gmt mapproject -Qe 2>&1 | grep TOPEX | awl '{TOPEX = %lf STO@a POP %lf INV 1 SUB NEG RCL@a MUL …\n", $3, $4} > grdmath.macros
and then just grdmath -R -I TOPEX = topex.grd
Or something like that.
1 Like
I’m afraid your solution is not correct. Your Earth is thinner at the equator and swelled at the poles when it should be the contrary.
1 Like
Yes, thanks Joaquim. I have to flip the values of the axis.