Examples showing the usage of grdmath

Showcase
1

After a recent question on the use of gmt math I decided to investigate the grdmath module which is analogous to math, but for operating on grids instead. And what I found was very pleasing, so here is a simple example to demonstrate the sorts of things it can do.

The example presented is computing relative humidity of the air from grids of temperature and dew-point temperature. Some meteorological models only provide the temperature and dew-point temperature, so if one wants relative humidity, it is necessary to compute it from these two related variables.

The way to compute relative humidity is to use this formula:

rh = 100\frac{e_{sat}(T_{d})}{e_{sat}(T)},

where rh is the relative humidity in %, T_{d} is the dew-point temperature in ℃, T is the temperature in ℃ and e_{sat}(T) is the saturation vapour pressure of water at temperature T.

There are several equations for computing saturation vapour pressure. Tetens’ equation is a simple one which has an accuracy better than ±0.1% at temperatures normally encountered near the Earth’s surface (there are complications with sub-zero temperatures which we will not discuss here):

e_{sat}(T) = 6.0178\exp\left(\frac{17.27T}{T+237.3}\right),

where e_{sat}(T) has units of hPa, and T has units of ℃.

Both math and grdmath support macros to simplify writing equations that use common formulae. So we start by defining some useful macros:

#!/usr/bin/env bash

# GMT grdmath macros.
cat << END > grdmath.macros
K2C = 273.15 SUB : Usage: tk K2C to return temperature in Celsius given temperature in Kelvin.
ESAT = STO@TC 17.27 MUL 237.3 RCL@TC ADD DIV EXP 6.1078 MUL : Usage tk ESAT to return saturation vapour pressure in hPa given temperature in Celsius using Tetens equation.
END

The first macro converts temperatures in Kelvin (the units usually used to disseminate temperature data) to Celsius. The second macro converts temperature in Celsius to saturation vapour pressure in hPa using Tetens’ equation.

I have gridded temperature and dew-point temperature data in NetCDF format from the European Centre for Medium-range Weather Forecasts. The grid extends from 180°W to 0° to 180°E, and from 90°S to 90°N, the spacing is 0,25° in both the longitude and latitude dimensions. The data are in a file called fld.nc, and the temperature and dew-point temperature variables are t2m and d2m respectively.

Here is the gmt grdmath command to compute the relative humidity (using the previously defined macros):

gmt grdmath fld.nc?d2m K2C ESAT fld.nc?t2m K2C ESAT DIV 100 MUL = rh_world.nc

And plotting it as well:

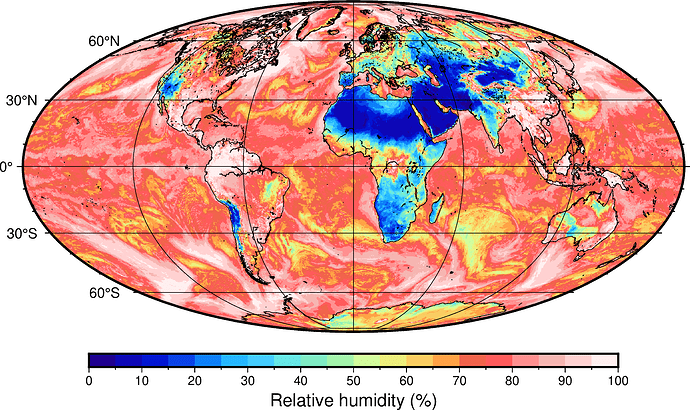
gmt begin rh_world PNG
	gmt grdmath fld.nc?d2m K2C ESAT fld.nc?t2m K2C ESAT DIV 100 MUL = rh_world.nc
	gmt makecpt -Chaxby -T0/100/5
	gmt grdimage rh_world.nc -JW15 -Rd -BWsen -Bpxf10a60g60 -Bpyf10a30g30
	gmt coast -Dl -Wthinnest,black
	gmt colorbar -Bpxf5a10+l"Relative humidity (%)" -DJCB+h+w12/0.3+jCT+o0/0.5
gmt end

rh_world
rh_world1848×1099 670 KB

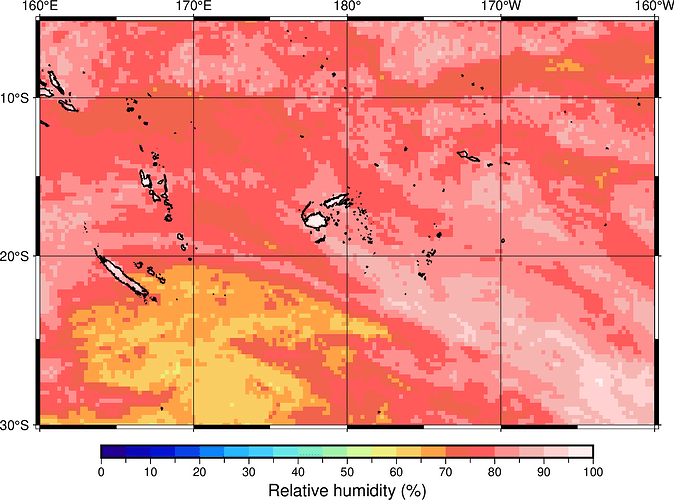
So far, so good. But here is the thing which really made me happy. The region I’m interested in crosses the International Dateline (180°E or thereabouts - it has some doglegs in it). Plotting data for an area which wraps from one edge of our grid to the other edge usually presents all sorts of hassles which need coding gymnastics to solve. But grdmath handles it seamlessly without any pain. Here is an example for the Southwest Pacific which crosses the edge of our grid:

gmt begin rh_swp PNG
	gmt grdmath -R160/200/-30/-5 fld.nc?d2m K2C ESAT fld.nc?t2m K2C ESAT DIV 100 MUL = rh_swp.nc
	gmt makecpt -Chaxby -T0/100/5
	gmt grdimage rh_swp.nc -JM15 -BWseN -Bpxf5a10g10 -Bpyf5a10g10
	gmt coast -Dh -Wthin,black
	gmt colorbar -Bpxf5a10+l"Relative humidity (%)" -DJCB+h+w12/0.3+jCT+o0/0.5
gmt end

rh_swp
rh_swp1945×1441 86.3 KB

There are more modern methods for doing this sort of computation - such as the Julia interface to GMT. But sometimes the old ways are pretty good too.

4 Likes
2

As alluded to in the previous post, there are other considerations when the temperature is below 0℃.

For temperatures greater than or equal to 0℃, Tetens’ equation above is used:

e_{sat}(T) = 6.0178\exp\left(\frac{17.27T}{T+237.3}\right).

For temperatures below 0℃, a modified equation is used:

e_{sat}(T) = 6.0178\exp\left(\frac{21.875T}{T+265.5}\right).

Here is a macro which computes e_{sat}(T) for temperatures above and below 0℃. It’s a bit messy, but it works:

ESAT = STO@TC 0 LT 21.875 17.27 IFELSE STO@A POP RCL@TC 0 LT 265.5 237.3 IFELSE STO@B POP RCL@TC RCL@A MUL RCL@TC RCL@B ADD DIV EXP 6.1078 MUL : Usage tk ESAT to return saturation vapour pressure in hPa given temperature in Celsius using Tetens equation.

What this does is save a variable called A for the coefficient on the top of the fraction (17.27 or 21.875) and another called B for the coefficient on the bottom of the fraction (237.3 or 265.5). The value of A and B are determined with the RPN fragments:

STO@TC 0 LT 21.875 17.27 IFELSE STO@A
and
RCL@TC 0 LT 265.5 237.3 IFELSE STO@B

These A and B coefficients are then used later in the equation. In practice there’s not much visible difference between the relative humidity computed using different e_{sat}(T) formulae for above and below 0℃.

One thing I discovered is that grdmath macros cannot refer to other macros. If this had been possible, then I could have made the macro for e_{sat}(T) much clearer than it is.

1 Like
3

Tim, you have to open a Weather Channel here in the Forum :smile:

2 Likes
4

And can’t resist to hijack a bit your post. With that other option, and only for the simpler case (other requires a lengthier fun)

julia> ecmwf(:forecast, vars=["2t", "2d"])
[ Info: Downloading 2t and saving to 2t_step0_ifs_oper_fc_20250601_00.grd
[ Info: Downloading 2d and saving to 2d_step0_ifs_oper_fc_20250601_00.grd

julia> T = gmtread("2t_step0_ifs_oper_fc_20250601_00.grd");
julia> Td = gmtread("2d_step0_ifs_oper_fc_20250601_00.grd");

julia> esat(x) = 6.0178*exp.(17.27*x ./ (x .+ 237.3))   # Define a function online
esat (generic function with 1 method)

julia> Grh = 100*esat(Td) / esat(T);

viz(Grh, proj=:guess, colorbar=true)
1 Like
5

Nices maps @timhume!!

I think that this example can be included here:
GMT Tutorials and Examples — GMT Examples documentation

1 Like
6

I was hoping you’d reply with something like this :grinning_face:

7

Yep, I felt the smell of the provocation :smile:

8

That’s the beauty of GMT. Not only can you use shell scripts, but nowadays you can use the Julia or Python interfaces too.

By the way, the just activated math plugin is great!

9

Please, don’t fall for the dark side. CLI is the way !

1 Like
10

There’s also gdal_calc.py: gdal_calc — GDAL documentation
“Command line raster calculator with numpy syntax”.

There are few examples on the docs web page, and I tried it but on small data sets in my texture shading scripts. Not sure how it works with a global grid that wraps around the globe.

It uses “normal” syntax rather than the RPN in grd math.