Grdmath D2DXY operator usage

Q&A
1

Hi, long-time user, first time poster here. Thanks to the GMT developers for all their effort on the software and also to this wonderful community that we have in the forum.

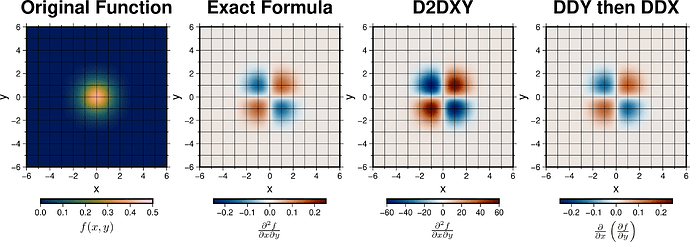
I just wanted to check whether the output of the D2DXY operator in grdmath is as intended. To demonstrate, I am including the following example script for a Gaussian function:

gmt begin gaussian_test_diff png

    # generate grid representation of a Gaussian function
    gmt grdmath -R-6.0/6.0/-6.0/6.0 -I0.05 2.0 PI MUL SQRT INV STO@nc POP \
        X Y HYPOT DUP MUL 2.0 DIV NEG EXP @nc MUL CLR@nc = gaussfunc.nc
    
    # generate meshes for the x and y coordinates
    gmt grdmath -R-6.0/6.0/-6.0/6.0 -I0.05 X = mesh_x.nc
    gmt grdmath -R-6.0/6.0/-6.0/6.0 -I0.05 Y = mesh_y.nc

    # exact solution for the derivative
    gmt grdmath gaussfunc.nc mesh_x.nc MUL mesh_y.nc MUL = d2gaussdxdy_ex.nc
    # compute derivative using the D2DXY operator
    gmt grdmath gaussfunc.nc D2DXY = gauss_d2dxy.nc
    # compute derivative using DDY and then DDX
    gmt grdmath gaussfunc.nc DDY DDX = gauss_ddx_ddy.nc

    # plot
    gmt subplot begin 1x4 -Fs6c -C0.25c

        gmt subplot 0,0

            gmt makecpt -Cbatlow -T0.0/0.5/0.01 -Z
            gmt grdimage gaussfunc.nc -Ba2f1g1 -BWeSn+t"Original Function" -Bx+l"x" -By+l"y"
        
            gmt colorbar -DJBC+o0c/1.25c+h -Ba0.1+l"@[ f(x,y) @[ "

        gmt subplot 0,1

            gmt makecpt -Cvik -T-0.25/0.25/0.01 -Z
            gmt grdimage d2gaussdxdy_ex.nc -Ba2f1g1 -BWeSn+t"Exact Formula" -Bx+l"x" -By+l"y"
        
            gmt colorbar -DJBC+o0c/1.25c+h -Ba0.1+l"@[ \frac{\partial^2 f}{\partial x \partial y} @[ "

        gmt subplot 0,2

            gmt makecpt -Cvik -T-60/60/5 -Z
            gmt grdimage gauss_d2dxy.nc -Ba2f1g1 -BWeSn+t"D2DXY" -Bx+l"x" -By+l"y"
        
            gmt colorbar -DJBC+o0c/1.25c+h -Ba20+l"@[ \frac{\partial^2 f}{\partial x \partial y} @[ "

        gmt subplot 0,3

            gmt makecpt -Cvik -T-0.25/0.25/0.01 -Z
            gmt grdimage gauss_ddx_ddy.nc -Ba2f1g1 -BWeSn+t"DDY then DDX" -Bx+l"x" -By+l"y"
        
            gmt colorbar -DJBC+o0c/1.25c+h -Ba0.1+l"@[ \frac{\partial }{\partial x } \left( \frac{\partial f}{\partial y} \right) @[ "

    gmt subplot end

gmt end show

I am also including the PNG file generated by the above script. The issue as I see it is that the values of the second partial derivative with respect to both x and y as computed by the D2DXY operator don’t seem to correspond with the exact formula (note the different ranges of the colorbars). However, applying the operators DDY then DDX seems to approximate the expected result.

I guess I was expecting all three approaches above to be equivalent within the numerical accuracy for computing derivatives using finite differences, so I am wondering whether the output from D2DXY is supposed to have these values.

Thanks for reading!

Cheers,
Soli

gaussfunc_test_diff
gaussfunc_test_diff3198×1122 168 KB

2

Can you fix the colorscale just to check ?

3

Funny, if we compute the ratio of the two solutions it gives 400 in all but edge cells

gmt grdmath gauss_d2dxy.nc gauss_ddx_ddy.nc DIV = d2ratio.grd

GMTjl_tmp
GMTjl_tmp1930×1746 39.2 KB

4

Thanks for the reply. Just to check, I have now used the same colorscale for all of the cases in computing of the derivative in in this version of the plot:

gaussfunc_test_diff_2
gaussfunc_test_diff_23198×1122 172 KB

5

Thank you for checking this ratio.

6

Good test @esmgarcia, I am looking into the coding - not a very often used operator (at least by me) and no test script in the suite so a bug might go undetected for a while…

7

So that’s why my rocket trajectory failed.

8

I notice that the 400 factor = 1/0.05 * 1/0.05 where the 0.05 are the grid steps.

9

PR submitted that solves the problem.

10

Thanks a lot to @Joaquim and @pwessel for looking into it and solving the problem!

I get why D2DXY isn’t probably used often, but I thought I’d bring it up anyway in case it was a bug.

11

And thanks for this exemplar post.