I am trying to use gmt regress for outlier detection and tried the different regression types (-Ex, -Ey, -Eo and -Er) on my dataset. I’m not an expert in statistics but I got forced to believe I get very strange-looking z-scores in some cases. In short, three regression types seemed to incorrectly assign outliers, namely, -Ex -N1, -Ex -N2, -Ex -Nr, and -Eo -N2 and this looks like a possible bug. Please see more below. I am sorry for this topic is so long.
My test data is a short incubation dataset, DIC (total carbonate) concentration (umol/L) vs sample time (min) that is supposed to grow linearly. Sample times were in chaotic order due to errors populating my database, so I added sort -n :
cat << EOF | sort -n > data.txt
680 1662.206718
350 1652.842149
1340 1677.668644
1010 1675.834363
2000 1712.388196
1670 1674.077904
2660 1730.88124
2330 1727.009523
EOF
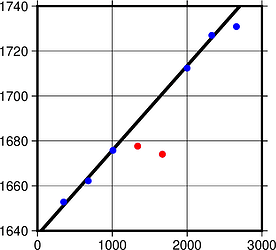
I tried all 12 combinations of -E(y|x|o|r) -N(1|2|r) like in gmt example 47. All 3 cases with -Ey looked OK so I’m skipping these here, just showing a plot for gmt regress data.txt -Ey -Nr showing the regression line, good points (blue circles) and outliers (red circles):
gmt begin test-Ey-Nr png
# plot the regression line using -Ey -Nr
gmt regress data.txt -Fxm -Ey -Nr -T0/3000/2+n | gmt plot -W2p -BWSen -Bxag -Byag -JX5c -R0/3000/1640/1740
#plot datapoints
gmt plot data.txt -Sc0.15c -Gblue -N
# plot outliers red
gmt regress data.txt -Fxy -Ey -Nr -Sr | gmt plot -Sc0.15c -Gred -N
gmt end show
corresponding regression data using -Fxymrwz:
gmt regress data.txt -Fxymrwz -Ey -Nr
> Best regression: N: 8 x0: 1505 y0: 1689.11 angle: 2.15625 E: 2.34152 slope: 0.0376514 icept: 1638.13 sig_slope: 0 sig_icept: 0 corr: 0.949391 R: 0.855974 N_eff: 8
350 1652.842149 1651.31194609 1.53020290613 1 0.367904050624
680 1662.206718 1663.73692091 -1.53020290613 1 -0.367904050624
1010 1675.834363 1676.16189572 -0.327532718379 1 -0.0787481276638
1340 1677.668644 1688.58687053 -10.9182265306 0 -2.62505041009
1670 1674.077904 1701.01184534 -26.9339413429 0 -6.47568115289
2000 1712.388196 1713.43682016 -1.04862415514 1 -0.252118900514
2330 1727.009523 1725.86179497 1.14772803261 1 0.275946275178
2660 1730.88124 1738.28676978 -7.40552977964 1 -1.78049877702
all looked good, the most suspected outliers at x=1340 and 1670 received the highest z-scores and labeled as outliers.
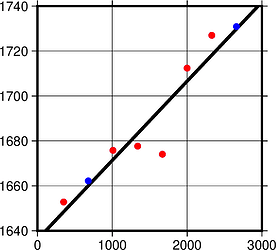
When I tried -Ex, things started looking strange. With -Ex -N1 the most suspected outlier at x=1670 did not get the highest z-score, lower than normal-looking points at the beginning, t=350, and at the end, t=2660 which does not look right. Signs of z-scores did not match signs of the corresponding regression errors for some points:
gmt regress data.txt -Fxymrwz -Ex -N1
> Best regression: N: 8 x0: 1505 y0: 1689.11 angle: 2.15272 E: 254.486 slope: 0.0375897 icept: 1631.97 sig_slope: 0 sig_icept: 0 corr: 0.949391 N_eff: 8
350 1652.842149 1645.12849718 7.71365182118 1 -1.77799181199
680 1662.206718 1657.53308909 4.67362891059 1 -1.34193006536
1010 1675.834363 1669.937681 5.896682 1 -0.906080295945
1340 1677.668644 1682.34227291 -4.67362891059 1 -0.469644113238
1670 1674.077904 1694.74686482 -20.6689608212 1 -0.0329381767597
2000 1712.388196 1707.15145673 5.23673926823 1 0.401684272597
2330 1727.009523 1719.55604864 7.45347435764 1 0.837484632166
2660 1730.88124 1731.96064055 -1.07940055296 1 1.2738195054
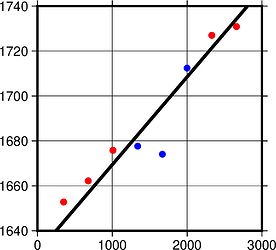
At -Ex -N2 z-scores were reversed, that is, the normal data points became outliers while the suspected outliers were not. Signs of z-scores did not match the signs of regression errors for some points:
gmt regress data.txt -Fxymrwz -Ex -N2
> Best regression: N: 8 x0: 1505 y0: 1689.11 angle: 2.23783 E: 75206.2 slope: 0.0390774 icept: 1630.3 sig_slope: 0.0126035 sig_icept: 9.04751 corr: 0.949391 N_eff: 8
350 1652.842149 1643.97916787 8.86298113042 0 -5.66277983016
680 1662.206718 1656.87471766 5.33200034316 0 -4.27482701374
1010 1675.834363 1669.77026744 6.0640955559 0 -2.88757563909
1340 1677.668644 1682.66581723 -4.99717323137 1 -1.49838379748
1670 1674.077904 1695.56136702 -21.4834630186 1 -0.108299328968
2000 1712.388196 1708.45691681 3.9312791941 1 1.27489079046
2330 1727.009523 1721.35246659 5.65705640684 0 2.66197866578
2660 1730.88124 1734.24801638 -3.36677638043 0 4.05083526994
On the plot it looked like this:
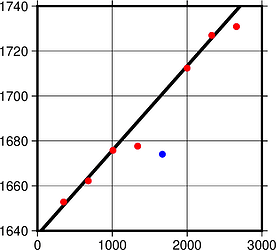
With -Ex -Nr the result was in principle the same nonsense, all points reported as outliers with very high z-scores except the most likely outlier point at x=1670. Signs of regression errors did not correspond to the signs of z-scores that looked strange:
gmt regress data.txt -Fxymrwz -Ex -Nr
> Best regression: N: 8 x0: 1505 y0: 1689.11 angle: 2.15272 E: 1635.15 slope: 0.0375897 icept: 1638.17 sig_slope: 0 sig_icept: 0 corr: 0.949391 N_eff: 8
350 1652.842149 1651.32213754 1.5200114553 0 -12.2852807436
680 1662.206718 1663.72672946 -1.5200114553 0 -9.28607208974
1010 1675.834363 1676.13132137 -0.296958365887 0 -6.28832140343
1340 1677.668644 1688.53591328 -10.8672692765 0 -3.28653739883
1670 1674.077904 1700.94050519 -26.8626011871 1 -0.282898042675
2000 1712.388196 1713.3450971 -0.95690109766 0 2.70641120392
2330 1727.009523 1725.74968901 1.25983399175 0 5.70382205202
2660 1730.88124 1738.15428092 -7.27304091884 0 8.70490925561
-Eo -N1 looked OK, no surprises, no points marked as outliers (so no plot shown), the most suspicious point assigned the highest z-scores, signs of z-scores always matched the signs of regression errors:
gmt regress data.txt -Fxymrwz -Eo -N1
> Best regression: N: 8 x0: 1505 y0: 1689.11 angle: 2.09375 E: 9.07272 slope: 0.0365591 icept: 1633.79 sig_slope: 0 sig_icept: 0 corr: 0.949391 N_eff: 8
350 1652.842149 1646.59024099 6.25190801391 1 0.489168298888
680 1662.206718 1658.65474599 3.55197200835 1 0.277917093655
1010 1675.834363 1670.719251 5.11511200278 1 0.400221921285
1340 1677.668644 1682.783756 -5.11511200278 1 -0.400221921285
1670 1674.077904 1694.84826101 -20.7703570083 1 -1.62513590771
2000 1712.388196 1706.91276601 5.47542998609 1 0.428414296247
2330 1727.009523 1718.97727102 8.03225198053 1 0.628467825953
2660 1730.88124 1731.04177603 -0.160536025035 1 -0.0125608268871
-Eo -N2 showed an issue: the z-scores were exactly equal to the residuals, so z-scores were not calculates as standardized values in this case. For this reason many points were labeled as outliers which is not correct. Plot not shown:
gmt regress data.txt -Fxymrwz -Eo -N2
> Best regression: N: 8 x0: 1505 y0: 1689.11 angle: 2.01752 E: 103.385 slope: 0.0352269 icept: 1636.1 sig_slope: 0.000461968 sig_icept: 1.96949e-16 corr: 0.949391 N_eff: 8
350 1652.842149 1648.42647317 4.41567582945 0 4.41567582945
680 1662.206718 1660.0513643 2.15535369961 1 2.15535369961
1010 1675.834363 1671.67625543 4.15810756976 0 4.15810756976
1340 1677.668644 1683.30114656 -5.63250256008 0 -5.63250256008
1670 1674.077904 1694.92603769 -20.8481336899 0 -20.8481336899
2000 1712.388196 1706.55092882 5.83726718024 0 5.83726718024
2330 1727.009523 1718.17581995 8.83370305039 0 8.83370305039
2660 1730.88124 1729.80071108 1.08052892055 1 1.08052892055
-Eo -Nr looked normal again, two outliers marked with z-scores looking good, the biggest outliers having the highest z-scores, the signs of the z-scores and the regression errors matched. The plot and equation are same as for the -Ey -Nr case, that looks sane:
gmt regress data.txt -Fxymrwz -Eo -Nr
> Best regression: N: 8 x0: 1505 y0: 1689.11 angle: 2.15625 E: 2.33821 slope: 0.0376514 icept: 1638.13 sig_slope: 0 sig_icept: 0 corr: 0.949391 N_eff: 8
350 1652.842149 1651.31194609 1.53020290613 1 0.368164734333
680 1662.206718 1663.73692091 -1.53020290613 1 -0.368164734333
1010 1675.834363 1676.16189572 -0.327532718379 1 -0.078803925783
1340 1677.668644 1688.58687053 -10.9182265306 0 -2.62691042733
1670 1674.077904 1701.01184534 -26.9339413429 0 -6.48026958997
2000 1712.388196 1713.43682016 -1.04862415514 1 -0.252297542989
2330 1727.009523 1725.86179497 1.14772803261 1 0.276141800883
2660 1730.88124 1738.28676978 -7.40552977964 1 -1.78176037505
-Er -N(1|2|r) look ok except no points received high enough z-scores to be marked as outliers. This is probably ok as signs of z-scores matched signs of the residuals and the greater residuals corresponded to the greater z-scores. No plots shown:
gmt regress data.txt -Fxymrwz -Er -N1
> Best regression: N: 8 x0: 1505 y0: 1689.11 angle: 2.09375 E: 47.4821 slope: 0.0365591 icept: 1633.79 sig_slope: 0 sig_icept: 0 corr: 0.949391 N_eff: 8
350 1652.842149 1646.59024099 6.25190801391 1 0.489168298888
680 1662.206718 1658.65474599 3.55197200835 1 0.277917093655
1010 1675.834363 1670.719251 5.11511200278 1 0.400221921285
1340 1677.668644 1682.783756 -5.11511200278 1 -0.400221921285
1670 1674.077904 1694.84826101 -20.7703570083 1 -1.62513590771
2000 1712.388196 1706.91276601 5.47542998609 1 0.428414296247
2330 1727.009523 1718.97727102 8.03225198053 1 0.628467825953
2660 1730.88124 1731.04177603 -0.160536025035 1 -0.0125608268871
gmt regress data.txt -Fxymrwz -Er -N2
> Best regression: N: 8 x0: 1505 y0: 1689.11 angle: 2.12468 E: 2862.57 slope: 0.0370998 icept: 1633.28 sig_slope: 0.000473617 sig_icept: 0.712793 corr: 0.949391 N_eff: 8
350 1652.842149 1646.26338054 6.5787684647 1 0.141982953182
680 1662.206718 1658.50629813 3.70041986764 1 0.0798624459333
1010 1675.834363 1670.74921573 5.08514727059 1 0.109747626887
1340 1677.668644 1682.99213333 -5.32348932647 1 -0.114891524129
1670 1674.077904 1695.23505092 -21.1571469235 1 -0.456613455424
2000 1712.388196 1707.47796852 4.91022747941 1 0.105972508694
2330 1727.009523 1719.72088612 7.28863688236 1 0.157303330369
2660 1730.88124 1731.96380371 -1.0825637147 1 -0.0233638855122
gmt regress data.txt -Fxymrwz -Er -Nr
> Best regression: N: 8 x0: 1505 y0: 1689.11 angle: 2.15625 E: 62.1894 slope: 0.0376514 icept: 1638.13 sig_slope: 0 sig_icept: 0 corr: 0.949391 N_eff: 8
350 1652.842149 1651.31194609 1.53020290613 1 0.0713880235114
680 1662.206718 1663.73692091 -1.53020290613 1 -0.0713880235114
1010 1675.834363 1676.16189572 -0.327532718379 1 -0.0152802698954
1340 1677.668644 1688.58687053 -10.9182265306 1 -0.509364221667
1670 1674.077904 1701.01184534 -26.9339413429 1 -1.25653978969
2000 1712.388196 1713.43682016 -1.04862415514 1 -0.0489210976804
2330 1727.009523 1725.86179497 1.14772803261 1 0.053544556378
2660 1730.88124 1738.28676978 -7.40552977964 1 -0.345487602923