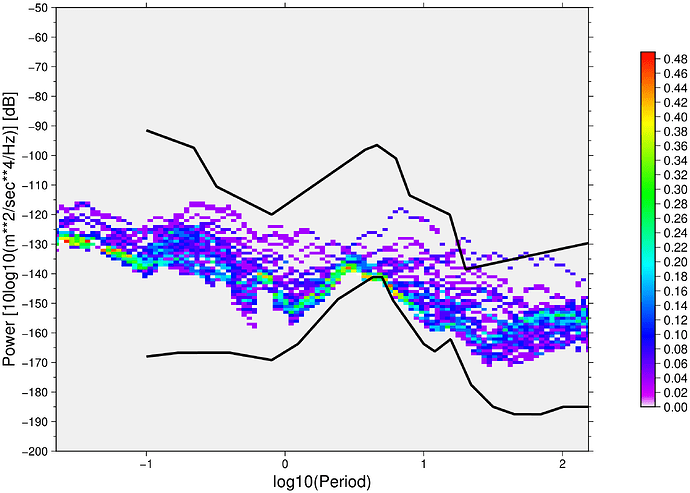
In seismology, we can use Power Spectral Density Probability Density Functions Calculation (usually abbreviated as PDF) described by McNamara 2004 in order to realize the status of instrument and what’s happening in the surrounding of the instrument.
For calculation, I have created a Julia package called SeisPDF.
For plotting, though the result is incorrect compared to the C version of SeisPDF, here is the function for creating the PDF plot:
"""
plot_pdf(pdf::Array{<:Real, 2}, center_periods::Array{<:Real, 1}; mindb::Real=-200, maxdb::Real=-50, db_interval::Real=1, kw...)
Plot PDF using GMT.jl.
# Arguments
- `pdf::Array{<:Real, 2}`: the matrix storing PDF.
- `center_periods::Array{<:Real, 1}`: the center periods.
# Optional
- `mindb::Real`: the minimum range of PDF. Measured in dB.
- `maxdb::Real`: the maximum range of PDF. Measured in dB.
- `db_interval::Real`: the interval of PDF. Measured in dB.
- `kw`: the keyword arguments passed to GMT.jl. For example:
- You can use `plot_pdf(pdf, center_periods; show=true)` just to show the graph.
- You can use `plot_pdf(pdf, center_periods; show=true, savefig="foo.png")` to show and save the graph to "foo.png".
- You can use `plot_pdf(pdf, center_periods; show=false, savefig="foo.png")` to just save the graph to "foo.png".
"""
function plot_pdf(pdf::Array{<:Real, 2}, center_periods::Array{<:Real, 1}; mindb::Real=-200, maxdb::Real=-50, db_interval::Real=1, kw...)
# Reverse the PDF matrix or the result will be up-side-down
reverse!(pdf, dims=1)
period_max = log10(maximum(center_periods))
period_min = log10(minimum(center_periods))
center_periods_interval_in_logscale = log10(center_periods[2]) - log10(center_periods[1])
pdf_min = minimum(pdf)
pdf_max = maximum(pdf)
# Create netCDF grid
pdf = reshape(pdf, :)
pdf_grid = xyz2grd(pdf,
R="$period_min/$period_max/$mindb/$maxdb",
I="$center_periods_interval_in_logscale/$db_interval",
Z="LBA")
high_noise_model = readdlm(high_noise_model_file)
low_noise_model = readdlm(low_noise_model_file)
high_noise_model[:, 1] = log10.(high_noise_model[:, 1])
low_noise_model[:, 1] = log10.(low_noise_model[:, 1])
# Plot
g_cpt = makecpt(color=cmap_file, T="$pdf_min/$pdf_max")
grdimage(pdf_grid,
J="X6i/5i",
frame=(axes=:WSne),
xaxis=(annot=1.0, label="log10(Period)"),
yaxis=(annot=10, ticks=5, label="Power [10log10(m**2/sec**4/Hz)] [dB]"),
color=cmap_file,
show=false)
colorbar!(g_cpt,
B=0.02,
pos=(anchor=:RM, offset=(1.5,0), neon=true),
show=false)
plot!(high_noise_model,
lw=2,
lc=:black,
show=false)
plot!(low_noise_model,
lw=2,
lc=:black;
kw...)
end
Below image shows the plotting of a certain input trace: