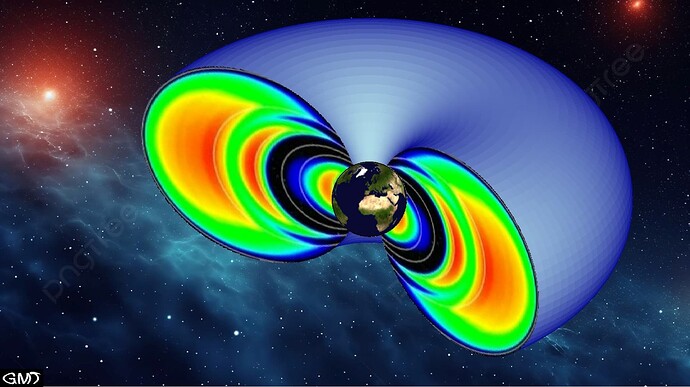
I’m looking to make a figure similar to the one below from GRACE Fact Sheet. Usually I might use grdview with -JZ and -p for a perspective view, but I’m not sure how to get that to work for a full hemispheric plot. Does anyone have any pointers for projections or module/flag combinations to try?
1 Like
Very interesting ! hummm it’s a good project for the weekend. I’ll try to reproduce it.
Getting closer 
It’s more difficult than I imagined. It is necessary to use a combination of grdview and perspective, but the orthographic projection gets in the way. Did you make progress on it @maxrjones ?
Did you make progress on it @maxrjones ?
No, it was just a side curiosity so I did not spend much time on it after the first post.
Not exactly good, but it’s something.
gmt begin geoid png
gmt makecpt -Cearth+h0 -T-6000/3000/100 -H > palette.cpt
gmt grdview -R-120/30/-60/60/-6000/3000 -JG-45/0/10c -JZ50c -Cpalette.cpt earth_coarse.nc -Qs -S4 -p189/89/0
# gmt coast -Di -A5000 -W -p
gmt end show
Adding illumination tends to improve things (in my personal opinion):
#!/usr/bin/env bash
gmt begin geoid ps
gmt grdview @earth_relief_15m -R0/360/-90/90/-6000/3000 \
-JG-45/0/10c -JZ30c -Cetopo1 -Qs -S4 -p189/89/0 -I
gmt end
gmt psconvert geoid.ps -E150 -Tg
Indeed 
Still, I don’t get why we need to tilt the view (-p) to get something not too messed up, nor why Antartica is like this…
I think it’s because the z-axis is perpendicular to the paper, not perpendicular to the surface of the Earth, which is really what we want.
Yes, I think grdview is basically a Cartesian operator. My hopes to solve this were to try to extend the triangular meshes example Subduction in Central America to a global extent.
Well, I kinda did it with grd2xyz then plot3d and the result is visually similar to grdview… with a lot more computation. 
(adapted from (8) A 3-D histogram — GMT 6.5.0 documentation)
2 Likes
I thought I had posted this example (from my AGU presentation) but I’m not finding it right now. Here the tube surface is made of triangles. I think it should work, but you are right that it will require a lot more of computations.
EDIT: It’s here Van Allen belt Basically it follows the Matlab’s FaceVertices method.
3 Likes